Lectura
e interpretación de gráficas
Al igual que muchos procesos matemáticos
utilizados en la escuela, la graficación comprende la interpretación y la
construcción. La interpretación se refiere a las habilidades de los estudiantes
para leer una gráfica tanto local como globalmente, y darle sentido o
significado (Leinhardt et al., 1990). En contraste, la construcción atañe al
acto de generar algo nuevo, construyendo una gráfica o trazando puntos a partir
de datos con una regla funcional o a partir de una tabla. Leindhart et al.
plantean que la construcción de una gráfica es completamente diferente de la
interpretación. Mientras que la interpretación ayuda y exige respuestas a
partir de datos dados (por ejemplo, una gráfica, una ecuación, o un conjunto de
datos), la construcción requiere generar partes nuevas que no están dadas.
La interpretación de gráficas precisa de
procesos agudos de visualización, aunque Eysemberg & Dreyfus (1991)
mostraron que muchos estudiantes poco utilizan el pensamiento visual. Prefieren
el trabajo algorítmico al pensamiento visual, ya que éste requiere de procesos
cognitivos superiores a los que demanda el pensamiento algorítmico.
Ahora bien, las interpretaciones de las
gráficas pueden estudiarse desde diferentes puntos de vista. Hay quienes
investigan las dificultades en la lectura de gráficas (Brassel & Rowe, 1993;
Moschkovich et al., 1993; Yerushalmi & Shternberg, 2001); en el caso de
Wainer (1992), identificó tres niveles de procesamiento de la información
relacionados con la interpretación gráfica:
a. El nivel elemental: Implica la
extracción de datos o la lectura de puntos aislados; por ejemplo, quién alcanzó
la más alta calificación del grupo, quién alcanzó la calificación más baja,
etc.
b. El nivel intermedio: Concierne a la
detección de las tendencias observadas en intervalos determinados de las
gráficas; por ejemplo, entre los años 1990 y 1993 qué compañía tuvo la razón
más grande de crecimiento.
c. El nivel más alto: Es una comprensión
profunda sobre la estructura de los datos y de su comportamiento; por ejemplo,
las muchachas crecen más rápido que los muchachos.
En otras investigaciones sobre el
pensamiento de los estudiantes de cálculo, cuando plantearon actividades de
interpretación en torno a lo cambiante de la razón de cambio se percibió que
esta habilidad es lenta de desarrollar; particularmente, se reportan problemas
al interpretar la información gráfica de una función (Carlson et al., 2002).
Muchas de estas dificultades están asociadas al escaso desarrollo de un
razonamiento covariacional, que se define como aquel que involucra a las
actividades cognitivas de coordinación de dos cantidades variables, atendiendo
las formas en que cambian una en relación con la otra. Como puede notarse, este
trabajo se orienta más hacia el estudio del pensamiento covariacional y tiene
similitud con la visión matemática de la graficación.
Según Cantoral & Montiel (2001), hay
dos formas clásicas de entender la enseñanza de la graficación: una asume que
la graficación es una técnica o conjunto de técnicas que permiten bosquejar la
gráfica de una función; otra, menos difundida, entiende la graficación como una
forma de interpretar el sentido y significado de sus propiedades desde una
perspectiva cognoscitiva. En tal enfoque se inserta nuestro trabajo.
Para explorar las interpretaciones que le
dan sentido y significado a las gráficas, adoptamos las acciones sugeridas en
el análisis de funciones planteadas en Dolores (1999), así como algunas
desprendidas de Carlson et al. (2002). Dichas acciones son congruentes con las
definiciones y objetivos de las gráficas de funciones que manejan los textos y
programas de estudio de matemáticas y de estadística. Una gráfica cartesiana se
define en los textos como una representación entre dos o tres variables, y se
considera como herramienta visual útil porque posibilita la detección de
tendencias, facilita las comparaciones y se constituye en un medio idóneo para
analizar el comportamiento de fenómenos de variación. Las acciones
sistemáticamente planteadas pueden resumirse en cinco: 1) ¿qué cambia?; 2)
¿cuánto cambia?; 3) ¿cómo cambia?; 4), ¿qué tan rápido cambia?; 5) ¿cómo se
comporta globalmente la gráfica?
La primera acción concierne a identificar
qué variables están representadas, ubicar puntos en el plano y determinar los
intervalos de variación. Para poder determinar cuánto cambia eso que cambia hay
que hacer comparaciones y operaciones de resta entre estados finales e iniciales,
tanto para la variable dependiente como para la independiente, atendiendo a la
correlación entre esos cambios. Para saber cómo cambian las variables
representadas, es preciso determinar si la gráfica crece, decrece o se mantiene
constante; en suma, la dirección del cambio. Para determinar la rapidez del
cambio se requiere emplear la razón promedio de cambio, que involucra
necesariamente cambios de la variable dependiente en relación con los de la
variable independiente. El comportamiento global y preciso de la gráfica
implica el uso de la razón de cambio instantánea (derivada) para precisar en
qué intervalos crece o decrece, en qué puntos tiene máximos, mínimos o puntos
de inflexión. Resulta claro que esta última no es tema de tratamiento en
primaria y secundaria, pues se reserva para el bachillerato y la universidad.
BIBLIOGRAFÍA
Cantoral, R. & Montiel, G. (2001).
Funciones: visualización y pensamiento matemático. México: Prentice Hall.
Cantoral, R. & Farfán, R. M. (2003).
Matemática educativa: una visión de su evolución. Revista Latinoamericana de
Investigación en Matemática Educativa 1(1), 27–40.
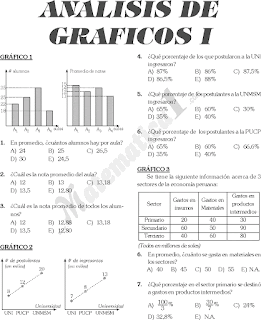
ANÁLISIS E INTERPRETACIÓN DE GRÁFICOS
EJEMPLOS

No hay comentarios:
Publicar un comentario